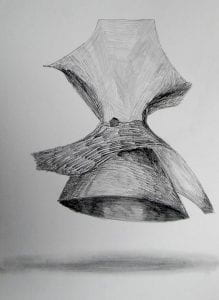
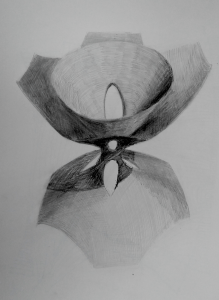
A collaborative artwork by Brendan Lancaster and Dr Florian Bouyer. It shows very many hand-drawn visualisations of K3 surfaces, on a large roll of wallpaper. Some examples are shown below.
These structures are of interest in the mathematical field of algebraic geometry, where they can be used to help mathematicians prove facts about whole numbers, using a geometric perspective. The surfaces that we encounter in our day-to-day lives are 2-dimensional. An example would be the wallpaper used in the pair’s artwork. If we imagine ourselves shrinking and standing at a corner of the wallpaper, we can move in 2 orthogonal directions: one for each edge of the paper. (We assume that the thickness of the paper is negligible, so we cannot really travel down, through the paper.) In contrast to this, the K3 surfaces used in Dr Bouyer’s research are 8-dimensional. While this sounds complicated, we must simply have the guts to imagine being able to head off 8 different directions rather than 2!
That said, if we wish to visualise these surfaces, it is challenging, because they do not really exist in our 3-dimensional world. Consequently, we can only glimpse sections of them at a time, called projections. This is for the same reason that we can only ever see the part of an object that faces our eye — it appears to us as a 2D picture, or projection, from the ambient 3D space that we live in.
The collaborators’ drawings use projections of their K3 surfaces, that may be obtained using computer software. They then interpret these on paper, effectively reprojecting them, through their own visual sense and aesthetic intuition.